
When you perform a rotation operation on a bitmap image, such as a digital photograph that you’re trying to straighten, you may sometimes create an undesirable effect called staircasing, where what were apparently straight and smooth edges in the original image become noticeably “stepped” in the rotated result. I noticed this problem recently when I tried to correct a shooting error in the image above (the version above shows the corrected image).
This article explains:
Staircasing: the Problem
Generally, whenever someone takes a photograph of a natural scene, they attempt to align the camera so that the ground line will appear exactly horizontal, and so that vertical edges in the scene will be truly vertical in the image.
However, the photographer doesn’t always achieve this, and that is becoming a more frequent problem in these days of smaller cameras. When you’re holding up your phone camera, it can be very difficult to ensure that it is exactly perpendicular to the horizon.
There are apps that you can install on your phone that display a “torpedo level” widget, so that you can determine when your device is exactly horizontal, but most people don’t use such apps. In any case, once a photo has been taken, you usually can’t go back and take it again.
Below is an example of an image where what should be vertical edges are not quite vertical, due to the angle at which the camera was held when the photograph was taken. I took this photo in London in 1981, and since then many of the buildings in the picture have been demolished, so there’s zero chance of being able to retake the photo!

If you look closely at the image above, you can see that what should be a vertical edge nearest to the centerline of the picture is not quite vertical. It’s tilted about 1° counter-clockwise. In theory, it’s easy to fix this by rotating the entire image 1° clockwise. However, if this is not done carefully, staircasing effects can result.
Below is an example of visible staircasing in a portion of the rotated image, resulting from an attempt to straighten the verticals in the original. (This is an enlargement to show the effect.) Notice the jagged transitions where the bright lamps contrast with the dark background.

How can you avoid this undesirable effect? Below, I offer a couple of solutions, but it’s important to bear in mind these overriding principles:
- Except for rotations in multiples of 90°, you should avoid rotating images unless absolutely necessary, because most rotations result in loss of detail.
- If you must rotate an image, perform only one rotation to achieve the final result, because each individual rotation introduces errors. For example, if you want to rotate your image by 3°, do that as one 3° operation rather than three consecutive 1° operations.
Staircasing: the Cause
As I explained in an earlier post, when you take a digital photograph, your camera creates a rectangular bitmap matrix of colored “dots” or pixels. The color value of each pixel is determined by the color of light shining on that particular detector in the sensor.
If you subsequently want to change the mapping of the color values to the bitmap matrix, as happens if you want to resize or rotate the image, then there has to be a way to determine the new color value of each pixel in the modified image.
The simplest way to determine the new color value of each pixel is simply to pick the value of the nearest corresponding pixel in the original image. (This is called Nearest-Neighbor Interpolation.) However, in areas of the image where there are sharp transitions of color, this method can lead to jagged edges and the effect called Staircasing.
(If you rotate a bitmap through some exact multiple of 90°, then this effect does not appear, because the original rectangular matrix maps exactly to a new rectangular matrix. The discussion here relates to rotations that are not a multiple of 90°.)
The following example shows a simple case of this problem. In these images, I’ve deliberately enlarged everything to the point that you can see the individual pixel boundaries; you would rarely see these at normal viewing magnifications. I’ve also tilted an edge that was originally vertical into a non-vertical position, rather than vice versa, because this shows the effect more plainly.
In the first image, on the left is the original unrotated image, which consists only of a dark rectangle abutting a light-colored rectangle. The transition between the two colors is a vertical edge, which maps neatly to the vertical alignment of the pixels.

On the right above is the result of rotating this image by 1 degree counter-clockwise, without any interpolation. Each new pixel takes the color value of the nearest pixel in the original image. Since the transition between the colors no longer maps neatly into vertically-aligned pixels, a jagged edge transition has now been created.
To reduce the quantization effects, a more sophisticated way of determining the new pixel values is by interpolation. Interpolation is basically a sophisticated form of averaging, whereby the color value of each interpolated pixel is determined by averaging the values of the nearest few pixels in the original image.
Here’s the same rotation operation, but with interpolation applied:
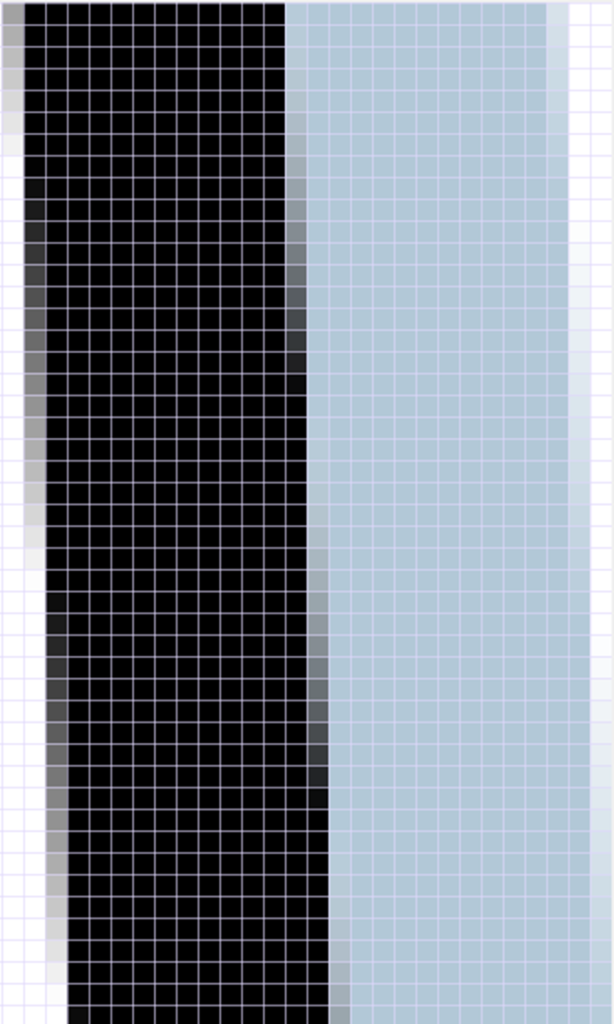
As you can see, the jaggedness is reduced, although there are still visible discontinuities, due to the small number of pixels involved.
Staircasing: the Solution
As demonstrated above, the staircasing effect is caused by inadequate interpolation of color values between adjacent pixels in a bitmap. If the interpolation could somehow be made perfect, the problem would not occur.
Typically, when we rotate an image, we’re using third-party software, and we’re stuck with whatever interpolation algorithm has been provided by the software manufacturer (which may consist of no interpolation at all). Thus, we can’t improve the interpolation, so all we can do is to take steps to disguise the problem.
Solution #1: Make Sure to Use Interpolation
Whenever you notice staircasing in a rotated image, the first thing to check is whether interpolation was applied during the rotation operation. Depending on the software you used to perform the rotation, interpolation may not have been applied by default, or, in the case of some low-end software, it may not even be available.
Look for an “interpolation” setting in your software. In some cases, this is referred to as “anti-aliasing”, even though there isn’t really any “aliasing” in this case. Make sure that “interpolation” or “anti-aliasing” are switched on.
Solution #2: Increase Image Resolution
If using interpolation doesn’t work, then the second approach is to try to reduce the quantization artefacts by temporarily increasing the Image Resolution. Most modern bitmap processing (“Paint”) software allows you to do this quite easily.
The procedure is as follows:
- Use your paint software to increase the image DPI. To minimize the amount of unnecessary interpolation required, it’s usually best to set the new DPI value to be an exact multiple of the current value. For example, if the image currently has 72 DPI, try increasing to four times that (288 DPI), or another higher multiple. (In general, the higher the DPI, the better, but of course increasing the resolution increases the total image size, so processing takes longer and requires more memory.)
- Perform the rotation operation.
- Reduce the image DPI back to the original value.
- Evaluate the results. If staircasing is still visible, repeat from Step 1, but this time increase the image DPI to an even higher multiple of the original.
Use Your Own Judgment
Ultimately, fixing this problem is a matter of aesthetic judgment; you have to view the results and decide when they’re good enough. What’s good enough in one situation may not be good enough in another.
I hope that my explanation has been helpful, but, if you need more detail, here is a very good post describing these concepts.
Definition: Image Size, Dimensions and Resolution
It may be helpful to remind ourselves of the differences between bitmap image size, dimensions and resolution. In my experience, these important distinctions can cause immense confusion to people working with bitmap images. That is not helped by the fact that some of these terms are used loosely and interchangeably in existing documentation, which merely adds to the confusion.
Each pixel in a bitmap image has a constant color value. The illusion that the colors in the image vary continuously occurs because the image typically consists of a very large number of pixels.
It’s intuitively obvious that each bitmap has a particular “size”, but what exactly does that term mean in this context? There’s more to it than just the number of pixels in the matrix, because that does not specify the size at which the bitmap is supposed to be viewed.
Note that these are my definitions of the terms, and you may find varying definitions in other documentation. The important point is to understand what is meant by each term, rather than which term is used for which concept.
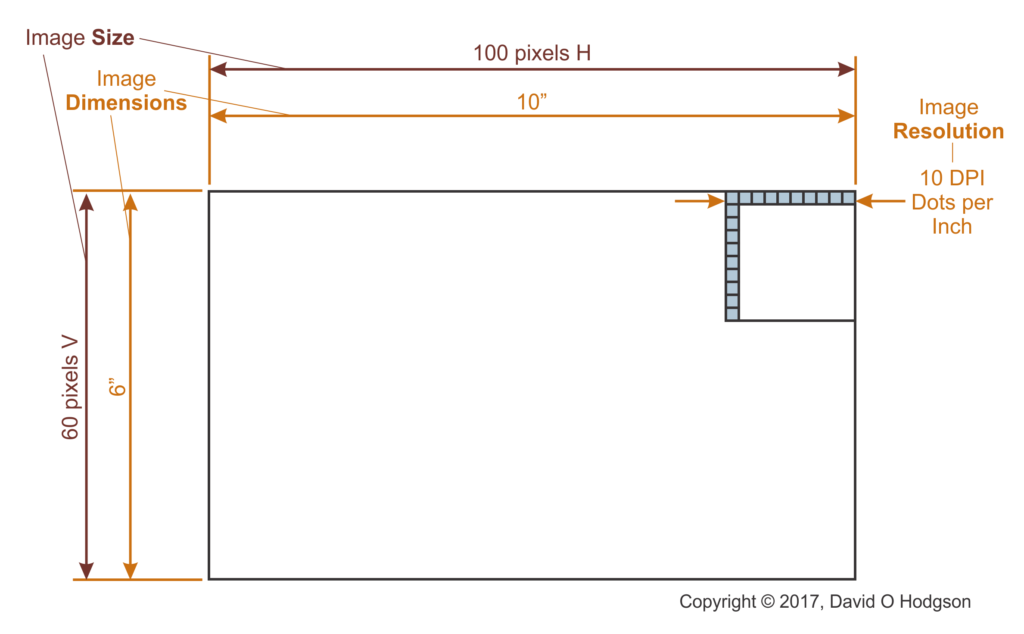
Image Size: The width and height of the image (W x H) in pixels
Image Dimensions: The width and height of the image (W x H) in measurement units
Image Resolution: Dots Per Inch. It is possible for an image to have different horizontal and vertical DPI values, but this is rarely done in practice. The horizontal and vertical resolutions are usually the same.
Definition: Interpolation
Interpolation is a mathematical concept, which involves creating new data points between the data points of an existing set.
When applied to images, interpolation usually involves creating a new pixel color value by averaging the values of nearby pixels, according to some algorithm.
